Donnerstag, 13.1.

Zusammenfassung:

Eine Mittelsenkrechte ist eine Gerade. Sie teilt eine Strecke in zwei genau gleich große Teile. Ihren Namen hat sie, weil sie immer senkrecht auf der Strecke steht, die sie teilt.

Beispiel:

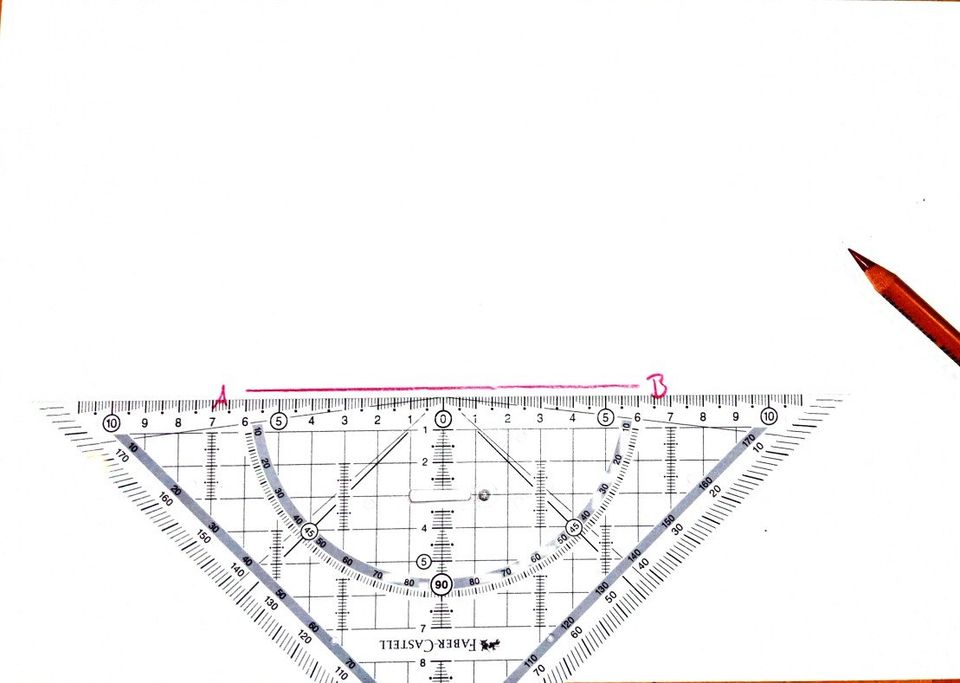
Wir möchten die Mittelsenkrechte auf der Strecke c=12 cm errichten. Die Strecke c wird links von A und rechts von B begrenzt:

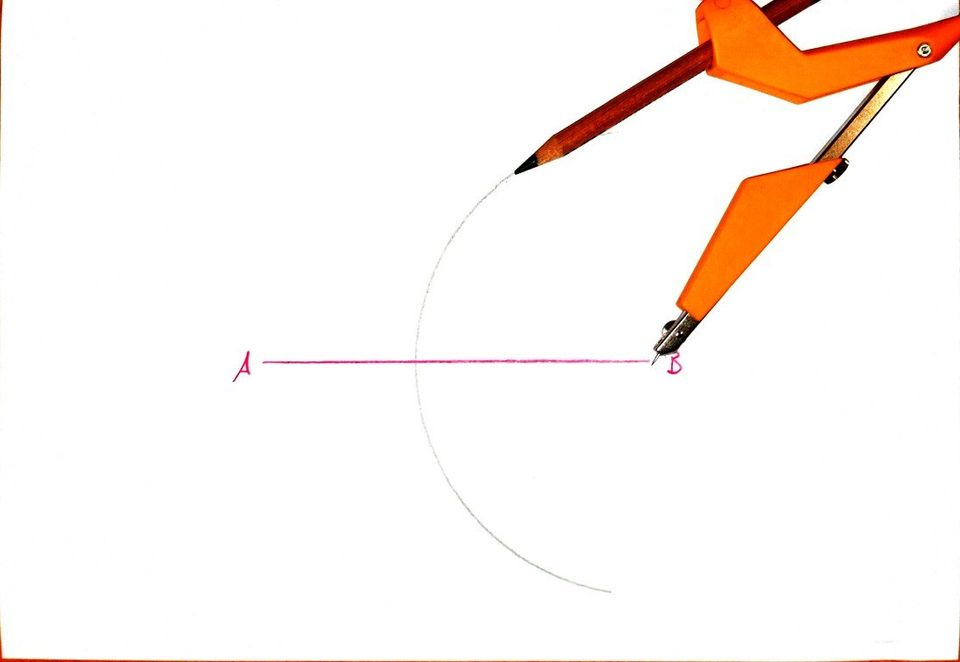
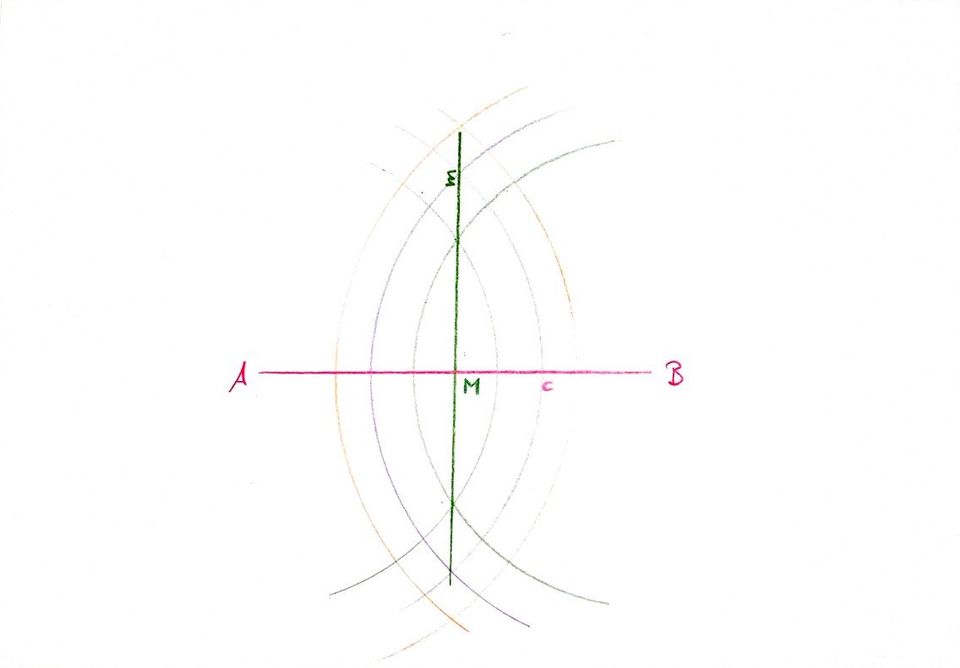
Wir ziehen um B einen großen Kreisbogen:

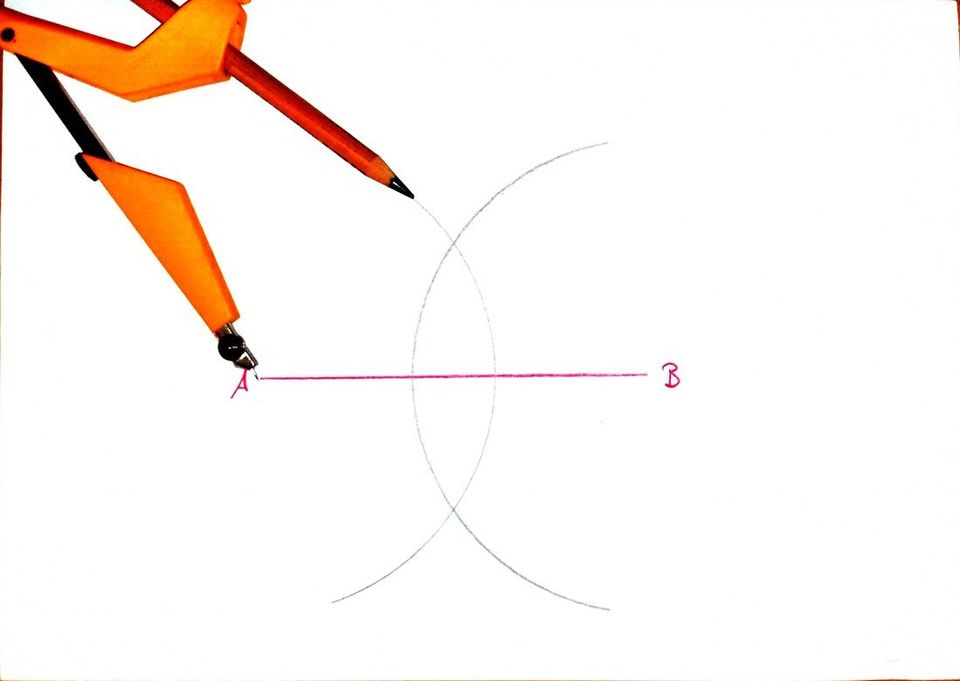
Wir ziehen um A einen Kreisbogen, der exakt denselben Radius hat:

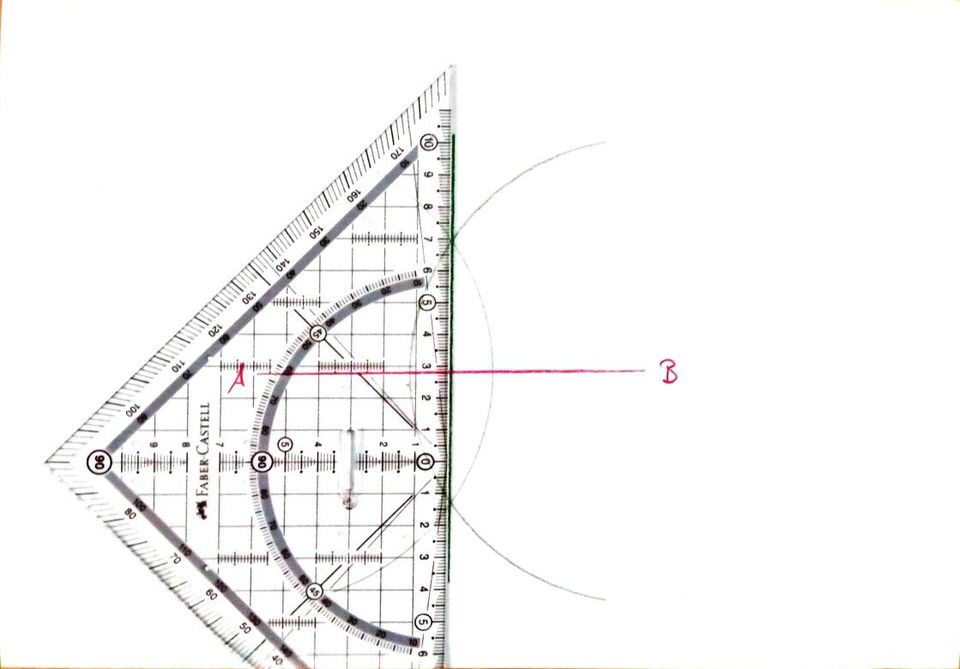
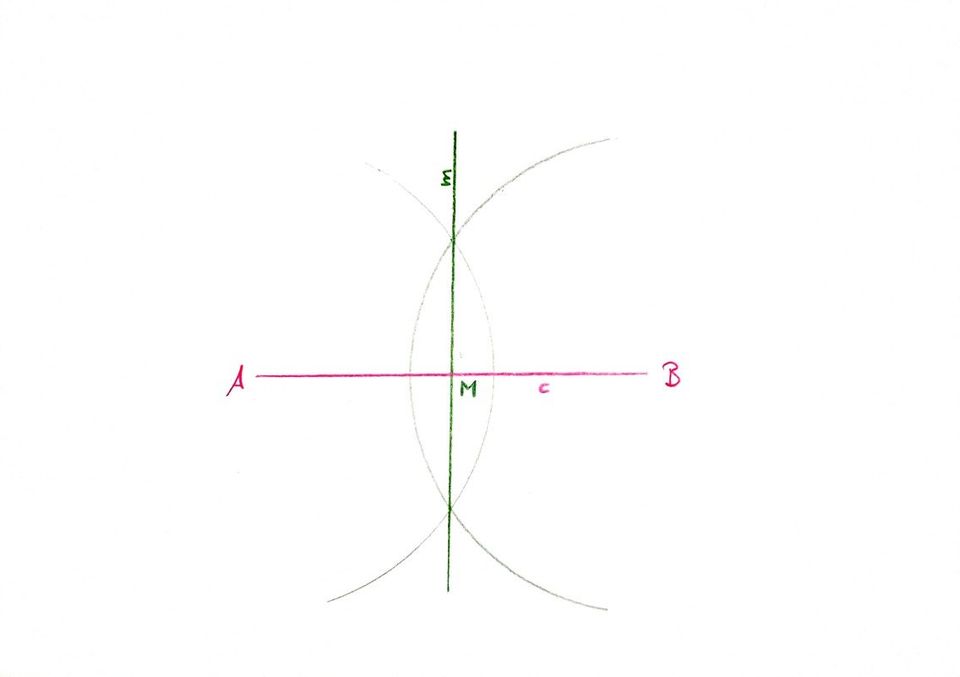
Wir verbinden die entstandenen Schnittpunkte:

Die entstandene Gerade nennen wir m und den nun entstandenen Schnittpunkt nennen wir M:

Geschafft!



Wie groß der Radius des Halbkreises ist, das ist übrigens egal. Er muss groß genug sein, dass sich beide Halbkreise deutlich überschneiden und: Der Radius des Kreisbogens um A und der Radius des Kreisbogens um B müssen exakt gleich groß sein:

Hausaufgabe für Donnerstag, 14.01.:

1.) Bearbeite das Kreuzworträtsel – findest Du alle Lösungen? 

2.) Bearbeite im Geometriearbeitsheft die Aufgaben 10a und 10b auf Seite 16.

3.) Zeichne im Geometriearbeitsheft auf Seite 10 sechs Strecken: a=10cm; b=15cm; c=12,5cm; d=10cm; e=15cm; f=12,5cm. Errichte auf den Strecken a, b und c die Mittelsenkrechten mit dem Zirkel. Errichte auf den Strecken d, e und f die Mittelsenkrechten mit dem Geodreieck, aber ohne Zirkel. Welche Methode findest Du praktischer und wieso?

4.) Fülle im Deutschhefter die Tabelle auf Seite 57 aus. Korrigiere dann eigenständig die Aufgaben 1-7 auf Seite 53-54 (HA von gestern). Gehe dabei genau so vor, wie wir es heute besprochen haben.

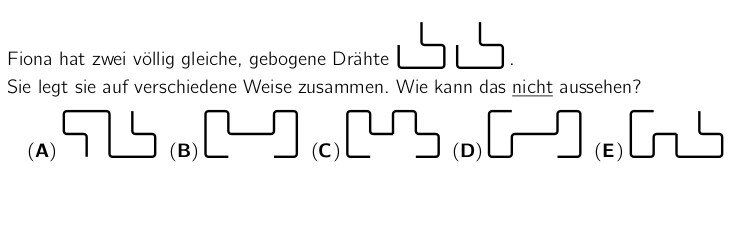
Und wer möchte, kann auch heute knobeln: